Question

Amanda is creating a rectangular garden in her back yard. The length of the garden is 14 feet. The perimeter of the garden must be at least 64 feet and no more than 96 feet.

Answer 1

`18\leq w\leq 34`

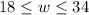
Explanation:

Please consider the complete question.

Amanda is creating a rectangular garden in her back yard. The length of the garden is 14 feet. The perimeter of the garden must be at least 64 feet and no more than 96 feet. Use a compound inequality to find the range of values for the width w of the garden.

Let w represent width of rectangular garden.

We know that perimeter of a rectangle is equal to 2 times the sum of length and width.

`\text{Perimeter}=2(l+w)`.

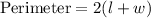We have been given that the perimeter of the garden must be at least 64 feet and no more than 96 feet. This means that perimeter should be greater than on equal to 64 and less than or equal to 96 feet.

We can represent this information in a compound inequality as:

`64\leq 2(l+w)\leq 96`

`64\leq 2(14+w)\leq 96`

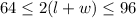
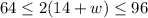
Let us solve for w as:

`(64)/(2)\leq (2(14+w))/(2)\leq (96)/(2)`

`32\leq 14+w\leq 48`

`32-14\leq 14-14+w\leq 48-14`

`18\leq w\leq 34`

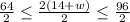
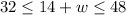
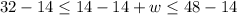
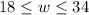
Therefore, the required range for width of garden would be
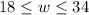`18\leq w\leq 34`.