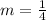(1) The train travels 4 miles per gallon.
(2) The slope of the graph is
Step-by-step explanation:
(1) The miles that train travels per gallon is given by
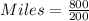
Dividing, we have,
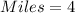
Thus, the train travels 4 miles per gallon.
(2) To determine the slope, let us consider two points from the graph.
The coordinates are
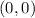 and
and
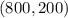
Thus, substituting the coordinates in the slope formula, we get,
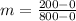
Simplifying, we have,
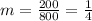
Thus, the slope of the graph is