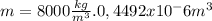Question

Suppose a soup can is made from a sheet of steel19 which is .13 mm thick. If the can is 11 cm high and 6 cm in diameter, use differentials to estimate the mass of the can. The density of the steel being used is 8000 kg/m3

Answer 1

The can mass is 0,00359 kg or 3,59 g

Step-by-step explanation:

1. Relevant Data:

Steel thickness= 0.13 mm or 0.013 mm

h=11 cm

d=6 cm

ρ=800 kg/m^3

2. Calculate mass from densisty equation:

`\rho=(m)/(v)`, then
`m=\rho .v`

We need to estimate the volume of the can to calculate the mass.

3. Estimate volume using differentials:

Cylinder volume equation is:

`V=(1)/(4)\pi d^(2)h`

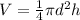
Considering that the can is an object with a hole inside, then we need to estimate the real volume of the sheet of steel.

Using differentials we have:

`dV=(1)/(2)\pi Dh (dD)`

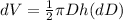
Then, we could say that
`dD=0.013 cm`

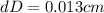
Replacing the values of d, h and dD, we obtain:

`dV=(1)/(6)\pi (6 cm)(11 cm)(0,013 cm)`

`dV=0,4492 cm^3`

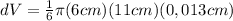
4. Calculate the mass

Convert volume unit into
`m^3`

`0,4492 cm^3x(1 m^3)/(1x10^6 cm^3) =0,4492 x 10^-6 m^3`

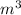
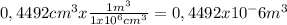
Calculate mass

`m=\rho .v`

`m=8000 (kg)/(m^3).0,4492 x10^-6 m^3`

`m=0,00359 kg =3,59 g`