Question

Approximately 80,000 marriages took place in the state of New York last year. Estimate the probabilitythat for at least one of these couples, (a) both partners were born on April 30; (b) both partners celebrated their birthday on the same day of the year. State your assumptions.

Answer 1

Explanation:

Given that there are 80000 marriages in Newyork last year

i.e. 80000 pairs were there

Each partner is independent of the other to have birthday.

Last year being 2019 was not a leap year so had 365 days

For any one to have Apr 30 as birth day = 1/365 (as all days are equally likely)

For couples together having same birth day would be

`((1)/(365) )^2`

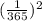
Out of 80000 each couple is independent of the other

X no of couples having birthday on Apr 30 is binomial with p = 1/365^2

Since n is very large we approximate to normal with

mean= 0.6005, and variance = np(1-p) = 0.6005

Std dev = 0.7749

a) Prob atleast one set of partners have Apr 30 as birthday

= P(X≥0)

= P(x≥-0.05) (with continuity correction)

= 1-0.2006

=0.7994

b) both partners celebrated their birthday on the same day of the year.

Here p will change to
`365*(1/365^2) = 1/365 = 0.00274`

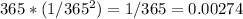
q= 0.99726

P(X
`\geq 0)`

X is normal with mean = 219.87 and std dev = 14.78

P(X>=-0.05) after continuity correction

=1

Almost certain event.