Question

A mass of 1.9 kg of air at 120 kPa and 24°C is contained in a gas-tight, frictionless piston–cylinder device. The air is now compressed to a final pressure of 600 kPa. During the process, heat is transferred from the air such that the temperature inside the cylinder remains constant. Calculate the work input during this process. Take the gas constant of air as R = 0.287 kJ/kg·K.

Answer 1

W=-260.66 kJ (negative answer means, that the work was done on the gas)

Step-by-step explanation:

1) Convert temperature from C to K- T=24+273=297K- all temperature in the gas problems should be used in Kelvins;

2) We need to analyse type of the process- it is given, that the temperature is constant, so it is an Isothermal process, which means, that the equation of the process is: pV=const (constant);

3) Work, done on the system, should be calculated using the following equation:
`W=\int\limits^(Vb)_(Va) {p} \, dV`

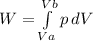
4) To calculate initical and final volumes (Va and Vb), we can use the following equation: pV=mRT, so V=mRT/p. Note, that the pressure is changing, thus we can calculate volumes for the both cases- initial and final, using initial (120kPa) and final (600kPa) pressures, in addition, we can find equation for the pressure, as function of the volume, which we need to use for the integration in step 3: p=mRT/V;

5) Now we can calculate the integral, given in the step 3:
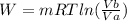`W=mRT ln((Vb)/(Va))`. As we have pressure as a known values, we can re-write the equation, using pressures:
`W=mRT ln((pa)/(pb))=1.9*0.287*279*ln((120)/(160))=-260.66 kJ`

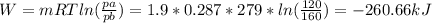
Note, that natural logarithm (ln) yields negative answer, which supports the question, that the work was done on the gas, not by the gas.