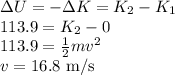Answer:
A) U1 = 135.6 J
B) U2 = 21.7 J
C) -113.9 J
D) 16.8 m/s
Step-by-step explanation:
The electric potential energy can be calculated by the following formula
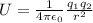
Since all the variables in the above formula are given, it is straightforward to calculate the electric potential energy in both cases.
A)
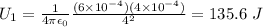
B)
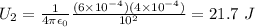
C) The change in the electric potential energy is equal to the difference between U1 and U2.
Therefore,
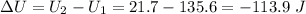
D) Since the change in the potential energy is fully converted into kinetic energy, therefore the change in the kinetic energy between both cases are equal to -113.9 J.