Answer:
Part a: There exists enough statistical evidence at 1% level of significance to show that the amount of time wasted in unsuccessful firms exceeds that of successful ones.
Part b: 95% Confidence interval for how much more time is wasted in unsuccessful firms than in successful ones is (2.3104, 3.2496) hours.
Step-by-step explanation:
Degrees of Freedom
df1 = n1 - 1 , df2 = n2 - 1 , df = n1 + n2 - 2
df = 398
Pooled Variance
The pooled variance is given as

By putting values in the formula,
Sp2 = 5.7401
Mean Squared Error Sm1-m2
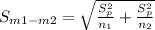
Putting values in the equation gives
Sm1-m2 = 0.2396
t-statistic
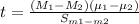
By putting in the values,
t-statistic = t = -11.6034
p-value
The p value for the t-static -11.6034 and df=398, from the t tables
p is found as 0.
Decision
0 < 0.01
that is p-value is less than alpha.
Hence we Reject the null hypothesis.
Conclusion
There exists enough statistical evidence at 1% level of significance to show that the amount of time wasted in unsuccessful firms exceeds that of successful ones.
Part b:
We find 95% confidence interval for μ2 - μ1
From the given data, for 95% Confidence interval
α = 0.05, α/2 = 0.025
From z tables for 95% confidence interval, z is given as 1.96.
Confidence interval is given by
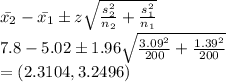
95% Confidence interval for how much more time is wasted in unsuccessful firms than in successful ones is (2.3104, 3.2496) hours.