Option D:
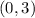 is the solution to the inequalities.
is the solution to the inequalities.
Step-by-step explanation:
From the given graph, we can see that the equation of the inequalities are
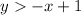 and
and
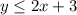
To determine the coordinate that satisfies the inequality, let us substitute the coordinates in both of the inequalities
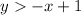 and
and

Thus, we have,
Option A:
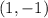
Substituting the coordinates in
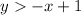 and
and
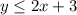 , we get,
, we get,
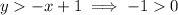 is not true.
is not true.
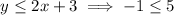 is true.
is true.
Since, only one equation satisfies the condition, the coordinate
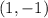 is not a solution.
is not a solution.
Hence, Option A is not the correct answer.
Option B:

Substituting the coordinates in
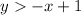 and
and
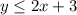 , we get,
, we get,
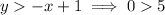 is not true.
is not true.
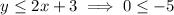 is not true.
is not true.
Since, both the equations does not satisfy the condition, the coordinate
 is not a solution.
is not a solution.
Hence, Option B is not the correct answer.
Option C:
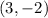
Substituting the coordinates in
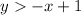 and
and
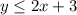 , we get,
, we get,
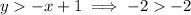 is not true.
is not true.
 is true.
is true.
Since, only one equation satisfies the condition, the coordinate
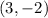 is not a solution.
is not a solution.
Hence, Option C is not the correct answer.
Option D:
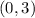
Substituting the coordinates in
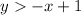 and
and
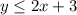 , we get,
, we get,
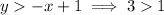 is true.
is true.
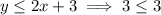 is true.
is true.
Since, both equation satisfies the condition, the coordinate
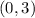 is a solution.
is a solution.
Hence, Option D is the correct answer.