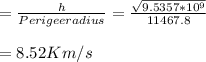Question

Ameteoroidisfirstobservedapproachingtheearthwhenitis402,000kmfromthecenterofthe earth with a true anomaly of 150 . If the speed of the meteoroid at that time is 2.23 km/s, calculate (a) the eccentricity of the trajectory; (b) the altitude at closest approach; and (c) the speed at the closest approach.

Answer 1

A. 1.086 B. 5089.8Km C. 8.52Km/s

Step-by-step explanation:

Energy

`E = (v^(2) )/(2) - (u)/((r)) \\\\E = (2.23^(2) )/(2) -(398000)/(402000) \\\\E = 2.48645 - 0.99\\E = 1.4964 Km^(2)/s^(2) \\`

`h^(2) = (-1)/(2) *(u^(2)* (1 -e^(2) ))/(E) \\\\h^(2) = (-1)/(2) *(398600^(2)* (1 -e^(2) ))/(1.4964)\\\\h^(2) = 5.309*10^(10) * (1 -e^(2) )`

`h^(2) = ur(1 + ecos (theta)) \\\\h^(2) = 398600 * 402000(1 + ecos (150))\\\\h^(2) = 16.02*10^(10) * (1 -0.866e )`

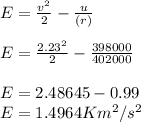
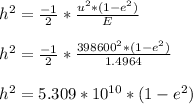
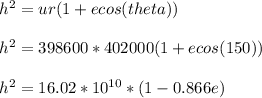
Equating both equations

`5.309*10^(10) * (1 -e^(2) )= 16.02*10^(10) * (1 -0.866e )\\\\1 -e^(2) = 3.018 * (1 -0.866e )\\\\0 = e^(2) + 2.613e - 4.018 \\\\e = -3.697 or 1.0861`

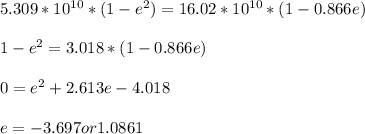
The eccentricity of the trajectory is taking to e the positive value i.e 1.0861

The altitude at closest approach is calculated from any of the two h^2 equations above

`h^(2) = 16.02*10^(10) * (1 -0.866e )\\\\h^(2) = 16.02*10^(10) * (1 -0.866 * 1.086 )\\\\h^(2) = 16.02*10^(10) * 0.059524\\\\h^(2) = 16.02*10^(10) * (1 -0.866e )\\\\h^(2)= 9.5357* 10^(9) Km^(4)/s^(2)`

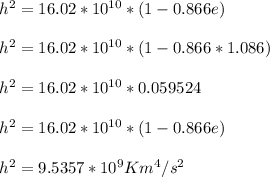
The perigee radius

`=(h^(2) )/(u) *(1)/((1+e )) \\\\=(h^(2) )/(u) *(1)/((1+e )) \\\\=(9.5357*10^(9) )/(398600) *(1)/((1+1.0861)) \\\\=(h^(2) )/(u) *(1)/((1-e^(2) )) \\\\=11467.8Km\\`

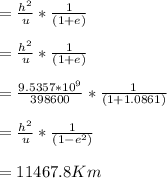
Note: radius of the earth = 6378Km

Perigee altitude = 11467.8 - 6378 = 5089.8 Km

c. speed

`=(h)/(Perigee radius) =\frac{\sqrt{9.5357*10^(9) } }{11467.8} \\\\= 8.52 Km/s`