Question

An alarming number of U.S. adults are either overweight or obese. The distinction between overweight and obese is made on the basis of body mass index (BMI), expressed as weight/height2. An adult is considered overweight if the BMI is 25 or more but less than 30. An obese adult will have a BMI of 30 or greater. According to a January 2012 article in the Journal of the American Medical Association, 33.1% of the adult population in the United States is overweight and 35.7% is obese. Use this information to answer the following questions.

a.
What is the probability that a randomly selected adult is either overweight or obese? (Round your answer to 3 decimal places.)



Probability


b.
What is the probability that a randomly selected adult is neither overweight nor obese? (Round your answer to 3 decimal places.)



Probability

Answer 1

(a) The probability that a randomly selected adult is either overweight or obese is 0.569.

(b) The probability that a randomly selected adult is neither overweight nor obese is 0.431.

Explanation:

Let A = a person is over weight and B = a person is obese.

The information provided is:

An adult is considered overweight if the BMI ≥ 25 but BMI < 30.

An obese adult will have a BMI ≥ 30.

According to the range of BMI the events A and B are independent.

P (A) = 0.331 and P (B) = 0.357.

(a)

Compute the probability that a randomly selected adult is either overweight or obese as follows:

P (A ∪ B) = P (A) + P (B) - P (A ∩ B)

= P (A) + P (B) - P (A)×P (B)

`=0.331+0.357-(0.331*0.357)\\=0.569833\\=0.569`

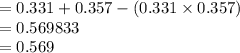
Thus, the probability that a randomly selected adult is either overweight or obese is 0.569.

(b)

Compute the probability that a randomly selected adult is neither overweight nor obese as follows:

`P(A^(c)\cup B^(c))=1-P(A\cup B)=1-0.569=0.431`

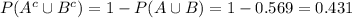
Thus, the probability that a randomly selected adult is neither overweight nor obese is 0.431.