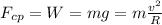Question

. A roller coaster contains a loop-the-loop in which the car and rider are completely upside down. If the radius of the loop is 10.0 m with what minimum speed must the car traverse the loop so that the rider does not fall out while upside down at the top

Answer 1

v=9.9m/s

Step-by-step explanation:

The centripetal force at the top of the loop is given by the weight of the car and the normal force. Since it is given by the equation
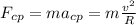`F_(cp)=ma_(cp)=m(v^2)/(R)`, the faster the car goes the higher the centripetal force needs to be, and this is given by the normal force. On the other hand, if the car slows down, the normal force will decrease, until the very limit when it is null and the centripetal force at the top of the loop would be given only by the weight of the car, and it cannot decrease further than this, so this minimal velocity is given by:

`F_(cp)=W=mg=m(v^2)/(R)`

`v=√(gR)=√((9.8m/s^2)(10m))=9.9m/s`