Question

A square has an area of 144 in^2. What is the length, to the nearest inch, of the diagonal?

Answer 1

The length of the diagonal is 17 in

Step-by-step explanation:

The area of the square =
`144 \ in^2`

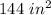
The formula for area of the square is given by

`A=a^(2)`

`144=a^(2)`

`12=a`

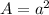
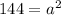
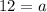
The sides of the square are 12 inches.

The length of the diagonal of a square can be determined using the Pythagorean theorem.

Let d be the diagonal of the square.

Thus, we have,

`$12^(2)+12^(2)=d^(2)$`

`144+144=d^(2)$`

`√(288) =d`

`16.97=d`

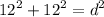
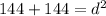
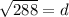
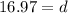
Rounding off to the nearest inch, we get,

`d=17 \ in`

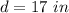
Thus, the length of the diagonal is 17 in