Question

The​ half-life of​ carbon-14 is 5600 years. If a piece of charcoal made from the wood of a tree shows only 66​% of the​ carbon-14 expected in living​ matter, when did the tree​ die?

The tree died about
? years ago
​(Do not round until the final answer. Then round to the nearest whole​ number.)

Answer 1

The tree died about 3357 years ago.

Step-by-step explanation:

The half life of carbon - 14 is given by

`A(t)=A(0)e^(-kt)`

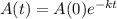
where
`A(t)=0.5`

`A(0)=1`

`t=5600`

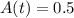
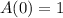
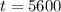
Substituting these values in the above equation, we get,

`0.5=1e^(-5600k)`

Taking In on both sides of the equation, we get,

`In(0.5)=-5600k`

`(In(0.5))/(-5600) =k`

`0.00012377=k`

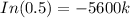
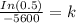
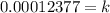
Since, only 66% of Carbon - 14 remains after the time T.

Thus, we have,

`0.66=1e^(-kT)`

Taking In on both sides of the equation, we get,

`In(0.66)=-0.00012377 \ T`

`(In(0.66))/(-0.00012377) = T`

`3357=T`

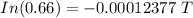
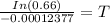
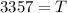
Thus, the tree died about 3357 years ago.