Question

Con ANB both have a volume of 48 pied Cubic units but have different dimensions Cohen a has a radius six units and a height for units find the one possible radius and height for can be to have the same volume as cone

Answer 1

Your question is difficult to understand, that is why I am going to edit your question as follow:

Edited Question:

Cone A and B both have a volume of 48π Cubic units but have different dimensions. Cone A has a radius=6 units and a height=4 units.

Find the one possible radius and height for cone B be to have the same volume as cone A.

Answer:

Radius of cone B= 6units

Height of cone B=units

Explanation:

As we know the formula for the volume of a cone is

`V=\pi\ r^(2)(h)/(3)`

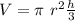
If volume of A and Volume B is given as same, thus

`V_(A)=V_(B)`

`\pi\ (R_(A)) ^(2)(H_(A) )/(3) =\pi\ (R_(B)) ^(2)(H_(B) )/(3)`

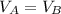
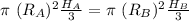
comparing equations above, we get

`R_(A)=R_(B)\\H_(A)=H_(B)`

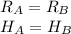
Thus, Radius of cone A=6units

and

Height of cone B= 4units