Question

A charged wire of negligible thickness has length 2L units and has a linear charge density λ. Consider the electric field E⃗ at the point P, a distance d above the midpoint of the wire.

Answer 1

The electric field at point P is
`2k\lambda d((L)/(d^2√(L^2+d^2)))`

Step-by-step explanation:

Given that,

Length = 2L units

Linear charge density = λ

We need to calculate the electric field at point P

Using formula of electric field

`E=2\int_(0)^(L){k(\lambda)/(r^2)dx\sin\theta}`

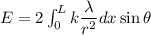
Put the value into the formula

`E=2k\int_(0)^(L){(\lambda)/((k^2+d^2))*(d)/(√(x^2+d^2))dx}`

`E=2k\lambda d\int_(0)^(L){\frac{dx}{(x^2+d^2)^{(3)/(2)}}}`

`E=2k\lambda d((x)/(d^2√(x^2+d^2)))_(0)^(L)`

`E=2k\lambda d((L)/(d^2√(L^2+d^2)))`

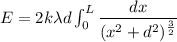
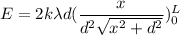
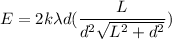
Hence, The electric field at point P is
`2k\lambda d((L)/(d^2√(L^2+d^2)))`