Question

Can someone help with this question? I only have 1 answer choice left

Answer 1

Option A:

Yes, he is correct.

Solution:

To find the distance between two points (2, 4) and (6, 3).

Distance between two points formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

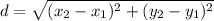
Here
`x_1=2, x_2=6, y_1=4, y_2=3`

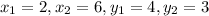
Substitute these in the distance formula.

Step 1:

`d=√((6-2)^2+(3-4)^2)`

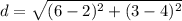
Step 2 :

Using BODMAS rule, first simplify the values into the bracket.

`d=√((4)^2+(-1)^2)`

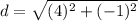
Step 3:

Squaring the numbers.

`d=√(16+1)`

`d=√(17)`

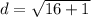
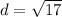
Therefore, George's work is correct.

Option A is the correct answer.