Answer:
Explanation:
Hello!
1) To test if a particular drug affects pilot reaction time to air traffic controller instruction.
The researcher sampled 10 pilots, first he recorded their normal performance and then the pilots were administered the drug and their reaction times were taken again.
The objective is to prove if the drug reduces the reaction time. There was only one sample taken and to every experimental unit (pilot) the reaction time before and after taking the drug was measured generating a paired sample data set, i.e. for each experimental unit there is a pair of values recorded. The statistic to use to test this claim is a paired sample t-test.
There are two variables of interest:
X₁: reaction time to air traffic control instructions of one pilot before taking the drug. (sec)
X₂: reaction time to air traffic control instructions of one pilot after taking the drug. (sec)
Since the variables are dependent you have to determine another one, usually referred to as "variable difference"
Xd: Difference between the reaction time to air traffic control instructions of a pilot before and after taking the drug. (X₁-X₂)
I've done a quick normality test, with a p-value 0.2303 against α: 0.05 the variable has a normal distribution so: Xd~N(μd;σd²)
If the drug does reduce the reaction time of the pilots, then the observations after taking it should be less than the observations before taking it and their differences positive, symbolically μd>0
Then the statistical hypotheses are:
H₀: μd ≤ 0
H₁: μd > 0
α: 0.05
![t= (Xd[bar]-Mud)/(Sd/√(n) ) ~t_(n-1)](https://img.qammunity.org/2021/formulas/mathematics/college/nodaan4rp51j25st8chibnq299o9hqxbh1.png)
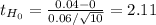
p-value:
P(t₉≥2.11)= 1 - P(t₉<2.11)= 1 - 0.9682= 0.0318
This test and it's p-value are one-tailed to the right (remember, the p-value always has the same direction as the test) The p-value is less than the significance level, so the decision is to reject the null hypothesis.
Then you can conclude with a level of 5% that the population average of the difference between the reaction time to air traffic control instructions of the pilots before and after they took the drug is greater than zero, I .e. the drug reduces the reaction time.
2)
The researcher's objective is to compare the flying hours of two groups of pilot students.
Group 1 represents the flying hours of pilot students that have at least a "B" average GPA.
Group 2 represents the flying hours of pilot students that have less than "B" average GPA
In this exercise the researcher took two samples of students, differentiated by their GPA score, and recorded their flying hours, these two groups determine two independent study variables:
X₁: Flying hours of a pilot student with a GPA score of at least "B"
X₂: Flying hours of a pilot student with GPA score below "B"
Using the data I've run a normality test:
X₁: p-value: 0.3448 vs. α: 0.05 ⇒ X₁~N(μ₁;σ₁²)
X₂: p-value: 0.8083 vs. α: 0.05 ⇒ X₂~N(μ₂;σ₂²)
Population variances are unknown and different.
To test the hypothesis that those students with a score equal or above "B" will have more flying hours than those students with a score below B you have to apply a pooled t-test for two independent variables.
H₀: μ₁ ≤ μ₂
H₁: μ₁ > μ₂
α: 0.05
![t= \frac{(X[bar]_1-X[bar_2])-(Mu_1-Mu_2)}{\sqrt{(S^2_1)/(n_1)+(S^2_2)/(n_2) } }](https://img.qammunity.org/2021/formulas/mathematics/college/otfz06blntyb0xlw4e12tl93eoot8i9351.png)
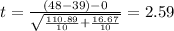
p-value: 0.0137
The p-value is less than α, the decision is to reject the null hypothesis.
At a 5% significance level, you can say that the average flying hours of pilot students with a GPA score of at least "B" is greater than the average flying hours of the pilot students with a GPA score of less than B.
I hope it helps!