Here is the full question with the appropriate tables.
Cortez Company is planning to introduce a new product that will sell for $108 a unit. The following manufacturing cost estimates have been made on 20,000 units to be produced the first year;
Direct Materials $700,000
Direct Labor $720,000 (= $18 per hour × 40,000 hours)
Manufacturing overhead costs have not yet been estimated for the new product, but monthly date on total production and overhead costs for the post 24 months have been analyzed using simple linear regression. The following results were derive from the simple regression and provide the basis for overhead cost estimates for the new product.
Simple Regression Analysis Results.
Dependent variable-Factory overhead cost-Independent Variable-Direct labor hours Computed values
Intercept $ 120,0000
Coefficient on independent variable $ 5.00
Coefficient of correlation .920
R² .828
What percentage of the variation in overhead costs is explained by the independent variable? 82.8% 91.1% 99.4% 74.5% None of the above.
What is the total overhead cost for an estimated activity level of 60,000 direct labor-hours?
$410,000.
$420,000.
$400,000.
$430,000.
Answer:
R² = 82.8%
$420,000
Step-by-step explanation:
Given that:
R² = .828
The percentage of the variation in overhead costs explained by the independent variable in Y from the X regressor =
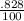 %
%
= 82.8%
Given that:
direct labor-hours = 60,000
To calculate the Total overhead cost; we have:
(Total overhead) to be = Estimated fixed cost + estimated variable cost per
labor hour × labor-hours
= Intercept estimate + Coefficient estimate on
independent variable × 60,000 direct labor-hours
= $120,000 + ($5 × 60,000) direct labor-hours
= $120,000 + $300,000
= $420,000
∴ the total overhead cost for an estimated activity level of 60,000 direct labor-hours = $420,000.