Question

A big clumsy cat having a mass of 4.00 kg falls from a tree branch for a distance of 2.00 m. In the air it rights itself and hits the ground with outstretched legs decelerating to a stop over a distance of 11.0 cm (from rest on the branch at the top, to crouched at rest on the ground the total distance covered is 2.00 m + 11.0 cm). Assuming a constant deceleration over the 11.0 cm, what force (in N) does the cat exert on the ground? (Hints: a kinematic equation used twice will get you most of the way there, and don’t forget about the cat’s weight.)

Answer 1

F = 752.68 N (force required to stop)

Step-by-step explanation:

Let's first find the total speed the cat was travelling at when it hit the ground.

This can be calculated by the following motion equation:

`v^2 - u^2 = 2*a*s`

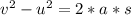
Here u = initial velocity = 0

a = acceleration due to gravity = 9.81 m/s

s = Distance covered from branch to ground = 2 m

Solving for v , we get 6.2641 m/s.

Let's solve the same motion equation again to find the deceleration required:

v^2 - u^2 = 2*a*s

where u = initial velocity = 6.2641 m/s

v = final velocity = 0 m/s

s = 0.11 m or 11 cm

Solving for a, we get - 178.36 m/s^2

Finally we can plug this acceleration into Newton's force equation : F = m*a

The force needs to incorporate the weight of the cat as well, so we can divide this into:

F1 = weight of cat = 4 * 9.81 = 39.24

F2 = average force required to stop

Newton's equation now becomes:

F1 - F2 = mass * acceleration

39.24 - F2 = 4 * (-178.36)

F2 = 752.68 N (force required to stop)