Option D:
The solution to the system of equations is (8, –12).
Solution:
Given system of equations are
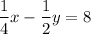 – – – – (1)
– – – – (1)
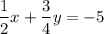 – – – – (2)
– – – – (2)
Lets simplify these equations.
In equation (1), take LCM of the denominator and make the same.
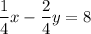
Do cross multiplication, we get
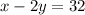
Add 2y on both sides of the equations.
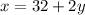 – – – – (3)
– – – – (3)
In equation (1), take LCM of the denominator and make the same.
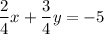
Do cross multiplication, we get
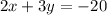 – – – – (4)
– – – – (4)
Substitute equation (3) in (4), we get
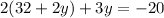
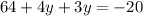
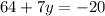
Subtract 64 from both sides of the equation.
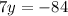
Divide by –7 on both sides of the equation.
y = –12
Substitute y = –12 in equation (3).
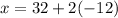
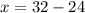
x = 8
The solution to the system of equations is (8, –12).
Hence option D is the correct answer.