Answer:
a) Therefore, the probability is P=0.28.
b) Therefore, the probability is P=0.42.
c) Therefore, the probability is P=0.54.
Explanation:
We know that A be the event that the selected student has a Visa card and B be the analogous event for MasterCard. Suppose that:
P(A) = 0.6 and P(B) = 0.3.
a) We calculate the probability that the selected student has neither type of card:
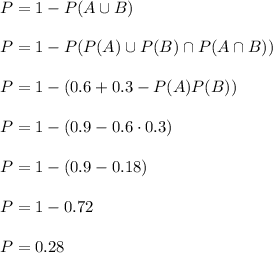
Therefore, the probability is P=0.28.
b) We calculate the probability that the select student has a visa card, but not a mastercard:
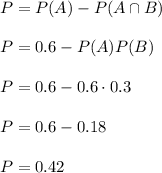
Therefore, the probability is P=0.42.
c) We calculate the probability that the selected student has exactly one of the two types of cards:
![P=[P(A)-P(A\cap B)]+[P(B)-P(A\cap B)]\\\\P=[0.6-0.18]+[0.3-0.18]\\\\P=0.42+0.12\\\\P=0.54](https://img.qammunity.org/2021/formulas/mathematics/college/kp11yb4f3q9uz9kkidfu1doitast3t1emm.png)
Therefore, the probability is P=0.54.