Question

(3 points) In Illinois, 9% of all drivers arrested for DUI (Driving Under the Influence) are repeat offenders; that is, they have been arrested previously for a DUI offence. Suppose 28 people arrested for DUI in Illinois are selected at random. You may assume that this is a binomial distribution. (0.5 pts.) a) What is the probability that exactly 3 people are repeat offenders

Answer 1

22.60% probability that exactly 3 people are repeat offenders

Explanation:

For each driver arrested selected, there are only two possible outcomes. Either they are repeat offenders, or they are not. The probability of an arrested driver being a repeat offender is independent from other arrested drivers. So we use the binomial probability distribution to solve this problem.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

In Illinois, 9% of all drivers arrested for DUI (Driving Under the Influence) are repeat offenders;

This means that
`p = 0.09`

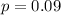
Suppose 28 people arrested for DUI in Illinois are selected at random.

This means that
`n = 28`

a) What is the probability that exactly 3 people are repeat offenders

This is
`P(X = 3)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 3) = C_(28,3).(0.91)^(25).(0.09)^(3) = 0.2260`

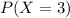
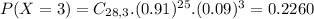
22.60% probability that exactly 3 people are repeat offenders