Question

An aluminum wire with a diameter of 0.125 mm has a uniform electric field of 0.305 V/m imposed along its entire length. The temperature of the wire is 45.0° C. Assume one free electron per atom.

(a) What is the current density in the wire?
(b) What is the total current in the wire?

Answer 1

(a) Current density is 1.05 x 10⁷ A/m²

(b) Total current in the wire is 0.129 A.

Step-by-step explanation:

As in the problem, the resistivity of aluminium is not mention. SO, we consider the case in which resistivity of aluminium is 2.65 x 10⁻⁸ ohm m at 20⁰ C.

The resistivity of the material depend upon the temperature by the equation:

р = р₀ [1 + α(T - T₀) ]

Here р is resistivity at temperature T, р₀ is resistivity at temperature T₀ and

α is constant.

Put 2.65 x 10⁻⁸ ohm m for р₀, 45° C for T, 20° C for T₀ and 3.9 x 10⁻³ /°C for α in the above equation.

р =
`2.65*10^(-8)(1 + 3.9*10^(-3)(45 - 20))`

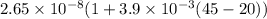
р = 2.90 x 10⁻⁸ ohm m

(a) The relation between electric field and current density is:

J = E/р

Substitute 0.305 V/m for E and 2.90 x 10⁻⁸ ohm m for р in the above equation.

J =
`(0.305)/(2.90*10^(-8) )`

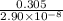
J = 1.05 x 10⁷ A/m²

(b) The relation between current and current density is :

I = J x A

Here A is the area.

Area of wire, A = π (d/2)²

Here d is the diameter of the wire.

So, I = J x π (d/2)²

Substitute 1.05 x 10⁷ A/m² for J and 0.125 x 10⁻³ m for d in the above equation.

I =
`1.05*10^(7)\pi((0.125*10^(-3))^(2) )/(4)`

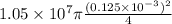
I = 0.129 A