SOLVING THE INEQUALITY
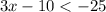 TO MATCH OPTION A
TO MATCH OPTION A
Considering the inequality
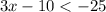
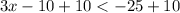
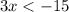
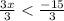
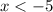
Thus,

Therefore, the inequality
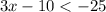 has the solution
has the solution
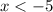 which matches the option A.
which matches the option A.
SOLVING THE INEQUALITY
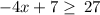 TO MATCH OPTION B
TO MATCH OPTION B
Considering the inequality
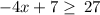
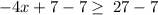
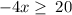
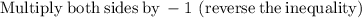
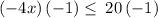
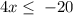
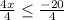
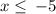
Thus,
![-4x+7\ge \:27\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\le \:-5\:\\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-5]\end{bmatrix}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/hoz68jdhix6m1j8ma7f8jt2ab2a6gp3tna.png)
Therefore, the inequality
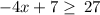 has the solution
has the solution
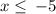 which matches the option B.
which matches the option B.
SOLVING THE INEQUALITY
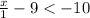 TO MATCH OPTION C
TO MATCH OPTION C
Considering the inequality
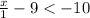
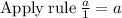
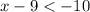 ∵
∵
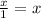
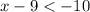

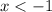
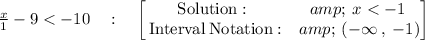
Therefore, the inequality
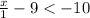 has the solution
has the solution
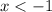 which matches the option C.
which matches the option C.
SOLVING THE INEQUALITY
 TO MATCH OPTION D
TO MATCH OPTION D
Considering the inequality
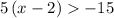
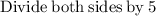
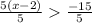
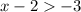
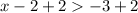
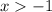
Thus,
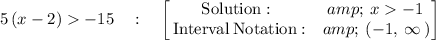
Therefore, the inequality
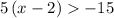 has the solution
has the solution
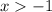 which matches the option D.
which matches the option D.