Question

On Friday night, the owner of Chez Pierre in downtown Chicago noted the amount spent for dinner for 28 four-person tables. 95 103 109 170 114 113 107 124 105 80 104 84 176 115 69 95 134 108 61 160 128 68 95 61 150 52 87 136 Click here for the Excel Data File (a) Find the mean, median, and mode. (Round your answers to 2 decimal places.) Descriptive Statistics Data Count Mean Median Mode (b) Are the data symmetric or skewed? If skewed, which direction? Symmetric Skewed left Skewed right

Answer 1

(a) The mean is 107.25, median is 106 and mode is 95.

(b) The data set is right-skewed.

Explanation:

The sample space of amount spent for dinner for 28 four-person tables is:

S = {95, 103, 109, 170, 114, 113, 107, 124, 105, 80, 104, 84, 176, 115, 69, 95, 134, 108, 61, 160, 128, 68, 95, 61, 150, 52, 87, 136}

There are n = 28 values in the set.

(a)

The mean of this data set is:

`\bar x=(1)/(n) \sum x=(1)/(28) *3003=107.25`

The mean is 107.25.

The data set consists of even number of observations.

The median for an even set of data is the mean of the middle two numbers.

First arrange the data set in ascending order:

52, 61 , 61 , 68 , 69 , 80 , 84 , 87 , 95 , 95 , 95 , 103 , 104 , 105 , 107 , 108 , 109 , 113 , 114 , 115 , 124 , 128 , 134 , 136 , 150 , 160 , 170 , 176

The median is the average value of the 14th and 15th observation.

`Median=(14^(th)obs.+15^(th)obs.)/(2)=(105+107)/(2)=106`

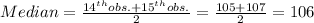
The median is 106.

The mode of a data set is the value with the most frequency.

Consider the arranged data set.

52, 61 , 61 , 68 , 69 , 80 , 84 , 87 , 95 , 95 , 95 , 103 , 104 , 105 , 107 , 108 , 109 , 113 , 114 , 115 , 124 , 128 , 134 , 136 , 150 , 160 , 170 , 176

The value 95 is repeated most of the times.

Thus, the mode is 95.

(b)

The value of mean, median and mode are related as follows:

Mean > Median > Mode

This implies that the data is skewed.

In case of a right-skewed data the Mean > Median > Mode.

In case of left skewed data the Mean < Median < Mode.

Thus, the data set is right-skewed.