Question

A production facility employs 10 workers on the day shift, 8 workers on the swing shift, and 6 workers on the graveyard shift. A quality control consultant is to select 5 of these workers for in-depth interviews. Suppose the selection is made in such a way that any particular group of 5 workers has the same chance of being selected as does any other group (drawing 5 slips without replacement from among 24).

(a) How many selections result in all 5 workers coming from the day shift?

(b)What is the probability that all 5 selected workers will be from the day shift? (Round your answer to four decimal places.)


(c) What is the probability that all 5 selected workers will be from the same shift? (Round your answer to four decimal places.)


(d) What is the probability that at least two different shifts will be represented among the selected workers? (Round your answer to four decimal places.)


(e) What is the probability that at least one of the shifts will be unrepresented in the sample of workers? (Round your answer to four decimal places.)

Answer 1

a) P=0.006

b) P=0.0059

c) P=0.0074

d) P=0.9926

e) P=0.3433

Explanation:

We know that a production facility employs 10 workers on the day shift, 8 workers on the swing shift, and 6 workers on the graveyard shift.

a) We calculate the probability that all 5 workers coming from the day shift.

We calculate the number of possible combinations:

`C_5^(24)=(24!)/(5!(24-5)!)=42504\\`

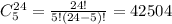
We calculate the number of favorable combinations:

`C_5^(10)=(10!)/(5!(10-5)!)=252`

Therefore, the probability is:

`P=(252)/(42504)\\\\P=0.006`

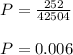
b) We calculate the probability that all 5 selected workers will be from the day shift.

We calculate the number of possible combinations:

`C_5^(24)=(24!)/(5!(24-5)!)=42504\\`

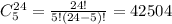
We calculate the number of favorable combinations:

`C_5^(10)=(10!)/(5!(10-5)!)=252`

Therefore, the probability is:

`P=(252)/(42504)\\\\P=0.0059`

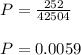
c) We calculate the probability that all 5 selected workers will be from the same shift.

We calculate the number of possible combinations:

`C_5^(24)=(24!)/(5!(24-5)!)=42504\\`

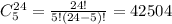
We calculate the number of favorable combinations:

`C_5^(10)+C_5^8+C_5^6=252+56+5=313`

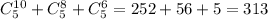
Therefore, the probability is:

`P=(313)/(42504)\\\\P=0.0074`

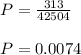
d) We calculate the probability that at least two different shifts will be represented among the selected workers.

So this is the opposite probability of the one we calculated in part (c).

Therefore, we get

P=1-0.0074

P=0.9926

e) We calculate the probability that at least one of the shifts will be unrepresented in the sample of workers.

Let
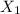`X_1` be the event that only day shifts be unrepresented.

Let
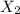`X_2` be the event that only swing shifts be unrepresented.

Let
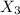`X_3` be the event that only graveyard shifts be unrepresented.

Therefore, we get:

`P(X_1\cup X_2\cup X_3)=P(X_1)+P(X_2)+P(X_3)-P(X_1\cap X_2)-P(X_1\cap X_3)--P(X_2\cap X_3)+P(X_1\cap X_2 \cap X_3)\\\\P(X_1\cup X_2\cup X_3)=0.0471+0.1028+0.2016-0.001-0.0013-0.0059+0\\\\P(X_1\cup X_2\cup X_3)=0.3433`

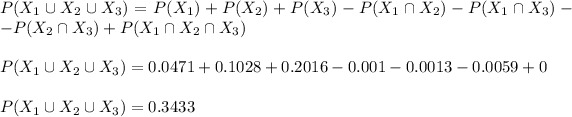
Threfore, the probabilty is P=0.3433.