Answer:

Explanation:
In the situation of this problem, we have:
- The initial college's tuition per hour is
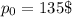
- Then, we know that the price increases by 5% each year. This means that its value increases by
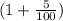 each year, which is equivalent to
each year, which is equivalent to
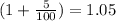 each year
each year
So, after 1 year, the price will be
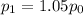
After 2 year, the price will be

So after n years, the price will be
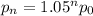
And by substituting the value of p0, we find the final expression:

where n is the number of years.