Question

Benzene, C6H6, and toluene, C6H5CH3, form an ideal solution. The vapor pressure of benzene is 94.6 Torr and that of Topic 5C Exercises 372 Topic 5C Phase Equilibria in Two-Component Systems toluene is 29.1 Torr at 25 8C. What is the vapor pressure of each component at 25 8C and what is the total vapor pressure of a mix- ture of 1.00 mol benzene and 0.400 mol toluene at 25 8C?

Answer 1

Answer: The vapor pressure of benzene and toluene at 25°C is 27.056 torr and 20.777 Torr respectively and the total vapor pressure of mixture is 47.833 Torr

Step-by-step explanation:

We are given:

Moles of benzene = 1.00 moles

Moles of toluene = 0.400 moles

Mole fraction of a substance is given by:

`\chi_A=(n_A)/(n_A+n_B)`

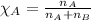
To calculate the vapor pressure of substance in a mixture, we use the equation given by Raoult's law, which is:

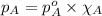`p_(A)=p_A^o* \chi_(A)` ........(1)

• For benzene:

`\chi_(benzene)=\frac{n_(benzene)}+{n_(benzene)+n_(toluene)}`

`\chi_(benzene)=(0.400)/(1.00+0.400)\\\\\chi_(benzene)=0.286`

Using equation 1, we get:

Vapor pressure of pure benzene = 94.6 Torr

Putting values in equation 1, we get:

`p_(benzene)=0.286* 94.6Torr\\\\p_(benzene)=27.056Torr`

• For toluene:

`\chi_(toluene)=\frac{n_(toluene)}+{n_(benzene)+n_(toluene)}`

`\chi_(toluene)=(1.00)/(1.00+0.400)\\\\\chi_(toluene)=0.714`

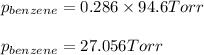
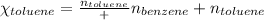
Using equation 1, we get:

Vapor pressure of pure toluene = 29.1 Torr

Putting values in equation 1, we get:

`p_(toluene)=0.714* 29.1Torr\\\\p_(toluene)=20.777Torr`

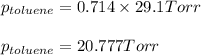
• Dalton's law of partial pressure states that the total pressure of the system is equal to the sum of partial pressure of each component present in it.

To calculate the total vapor pressure of the mixture, we use the law given by Dalton, which is:

`P_T=p_(toluene)+p_(benzene)`

`P_T=20.777+27.056\\\\p_T=47.833Torr`

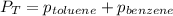
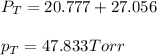
Hence, the vapor pressure of benzene and toluene at 25°C is 27.056 torr and 20.777 Torr respectively and the total vapor pressure of mixture is 47.833 Torr