Question

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 150 lb and 201 lb. the new population of pilots has normally distributed weights with a mean of 160 lb and a standard deviation of 27.5 lb.

A.) if a pilot is randomly selected, find the probability that his weight is between 150 lb and 201 lb.
The probability is approximately__________. (round to four decimal place as needed.)
B.) If 39 different pilots are randomly selected, find the probability that their mean weight is between 150 lb and 201 lb.
The probability is approximately__________. (round to four decimal place as needed.)
C) When redesigning the ejection seat which probability is more relevant
Part A or Part B

Answer 1

A) 0.5737

B) 0.9884

Explanation:

We are given that an engineer is going to redesign an ejection seat for an airplane. The new population of pilots has normally distributed weights with a mean of 160 lb and a standard deviation of 27.5 lb i.e.;
`\mu` = 160 lb and
`\sigma` = 27.5 lb

(A) We know that Z =
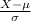`(X - \mu)/(\sigma)` ~ N(0,1)

Let X = randomly selected pilot

If a pilot is randomly selected, the probability that his weight is between 150 lb and 201 lb = P(150 < X < 201)

P(150 < X < 201) = P(X < 201) - P(X <= 150)

P(X < 201) = P(
`(X - \mu)/(\sigma)` <
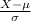`(201 - 160)/(27.5)` ) = P(Z < 1.49) = 0.9319

P(X <= 150) = P(
`(X - \mu)/(\sigma)` <
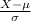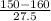`(150 - 160)/(27.5)` ) = P(Z < -0.3636) = P(Z > 0.3636) = 0.3582

Therefore, P(150 < X < 201) = 0.9319 - 0.3582 = 0.5737 .

(B) We know that for sampling mean distribution;

Z =
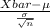`(Xbar - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

If 39 different pilots are randomly selected, the probability that their mean weight is between 150 lb and 201 lb is given by P(150 < X bar < 210);

P(150 < X bar < 210) = P(X bar < 201) - P(X bar <= 150)

P(X bar < 201) = P(
`(Xbar - \mu)/((\sigma)/(√(n) ) )` <
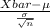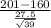`(201 - 160)/((27.5)/(√(39) ) )` ) = P(Z < 9.311) = 1 - P(Z >= 9.311)

= 0.999995

P(X bar <= 150) = P(
`(Xbar - \mu)/((\sigma)/(√(n) ) )` <
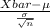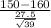`(150 - 160)/((27.5)/(√(39) ) )` ) = P(Z < -2.2709) = P(Z > 2.2709)

= 0.0116

Therefore, P(150 < X bar < 210) = 0.999995 - 0.0116 = 0.9884

C) If the tolerance level is very high to accommodate an individual pilot then it should be appropriate ton consider the large sample i.e. Part B probability is more relevant in that case.