Answer:
9.852
Explanation:
First, Graph all three functions and find where they intersect and the shape that they make through their intersection. Note that since the shape does not touch the y= -1 line, we will use the "washer" method (where the volume equals
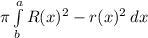 .
.
The next step is to find a and b. Since the function that the area is going to be rotated about is a " y =" equations, the boundaries will be the x coordinates where the three functions intersect, b=1 for (1,1) and a=3 for (3,1).
Next we have to find R(x) and r(x). In this case, R(x) is the difference between the function furthest away from the axis of rotation and the function of the axis of rotation (or visa versa depending on which is on top), and r(x) is the difference between the function closest to the axis of rotation and the function of the axis of rotation (or visa versa depending on which is on top.
For this problem R(x) = 1 - (-1) and r(x) = 1/x - (-1) since when you look at the graph, Y = 1 is further from y = -1 than y = 1/x is, and both functions are on top of y = -1.
Finally plug in R(x) and r(x) and solve either using a calculator or through integration. If you solve through integration you should get
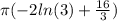 .
.