Question

The area enclosed by the graphs of y = 1/x, y = 1, and x = 3 is rotated about the line y = -1. Find the volume and show steps.

Answer 1

`A=\pi\displaystyle\biggr[(16)/(3)-2\ln(|3|)\biggr]\approx9.8524`

Explanation:

Use the Washer Method
`A=\pi\displaystyle \int\limits_(a)^(b){\bigr[R(x)^2-r(x)^2\bigr] \, dx` where
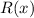`R(x)` is the outer radius and
`r(x)` is the inner radius.

If we sketch out the graph, we see that
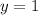`y=1` intersects points
`(1,1)` and
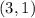`(3,1)`, which will be our bounds of integration.

Here, our outer radius will be
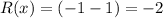`R(x)=(-1-1)=-2` and our inner radius will be
`r(x)=-1-(1)/(x)`.

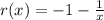Thus, we can compute the integral and find the volume:

`A=\pi\displaystyle\int\limits^(3)_(1) {(-2)^2-\biggr(-1-(1)/(x)\biggr)^2 } \, dx\\ \\A=\pi\displaystyle\int\limits^(3)_(1) {4-\biggr(1+(2)/(x)+(1)/(x^2) \biggr) } \, dx\\\\A=\pi\displaystyle\int\limits^(3)_(1) {4-1-(2)/(x)-(1)/(x^2)} \, dx\\\\A=\pi\displaystyle\int\limits^(3)_(1) {3-(2)/(x)-(1)/(x^2)} \, dx\\\\A=\pi\displaystyle\biggr[3x-2\ln(|x|)+(1)/(x)\biggr]\Biggr|_(1)^(3)\\`

`A=\pi\displaystyle\biggr[\biggr(3(3)-2\ln(|3|)+(1)/(3)\biggr)-\biggr(3(1)-2\ln(|1|)+(1)/(1)\biggr)\biggr]\\\\A=\pi\displaystyle\biggr[\biggr(9-2\ln(|3|)+(1)/(3)\biggr)-\biggr(3+1\biggr)\biggr]\\\\A=\pi\displaystyle\biggr[\biggr((28)/(3)-2\ln(|3|)\biggr)-\biggr(4\biggr)\biggr]\\A=\pi\displaystyle\biggr[(16)/(3)-2\ln(|3|)\biggr]\\A\approx9.8524`

In conclusion, the volume of the solid of revolution will be about 9.8524 cubic units. See the attached graph for a helpful visual!