Answer:
-7
Explanation:
Here we want to find the point that divide the segment AB into ratio 3:4.
The coordinates of A are
A (-4, -10)
B (-11, -7)
We can use the formula
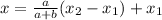
In order to find the x-coordinate of the point that divides AB into a 3:4 ratio.
In this problem, we have:
a = 3
b = 4
where a/b = 3/4 is the ratio, and

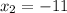
Are the coordinates of the endpoints
Substituting into the formula, we find
