Question

A lake contains an amount V liters of water. Initially, the water contains an amount P liters of a pollutant. Water is flowing into the lake at a rate of F liters per second, and well mixed lake fluid is flowing out at the same rate. The ratio of pollutant to total fluid in the inflow is r. The amount of p(t) of pollutant in the lake is:_________

Answer 1

The quantity of P(t) in the lake is
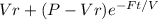`Vr+(P-Vr)e^(-Ft/V)` litres where V is the amount of water in litres, r is the concentration of the flow in, P is the initial amount , F is the rate of flow in/out and t is time.

Explanation:

The equation is given

Rate of Change of Amount=Flow Rate(in)*(Conc. of flow in)-Flow Rate(out)*(Conc. at any given time)

Here

Change of Amount is given P'(t)

Flow Rate(in) and Flow Rate(out) are given F

The conc. at any time is given P(t)/V

The conc. of the Flow in is given r

The initial concentration is given P

so the equation becomes

`P'(t)=rF-(P(t))/(V)F`

Now this equation in the standard form of the linear differential equation is as below and the integrating factor is

`x'(t)=b+a(x)x(t)\\`

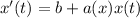
Here

`a(x)=-(F)/(V)`

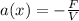
So integrating factor is

`e^(Ft/V)`

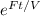
Now the equation is

`P(t)=e^(-Ft/V) * \int{e^(F/V)Frdt} \\P(t)=e^(-Ft/V) *[Fr(V)/(F)e^(Ft/V)+C]\\P(t)=Vr+Ce^(-Ft/V)`

As the initial condition is

As P(0)=P so by substituting this in the equation gives

`P(t)=Vr+Ce^(-Ft/V)\\P(0)=Vr+Ce^(-F(0)/V)\\P=Vr+C\\C=P-Vr`

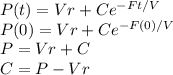
Putting this in the above differential equation

`P(t)=Vr+Ce^(-Ft/V)\\P(t)=Vr+(P-Vr)e^(-Ft/V)`

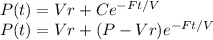
So the amount P(t) in the lake is
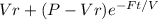`Vr+(P-Vr)e^(-Ft/V)` litres where V is the amount of water in litres, r is the concentration of the flow in, P is the initial amount, F is the rate of flow in/ out and t is time.