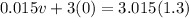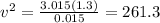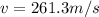Question

A 15g bullet is fired horizontally into a 3kg block of wood suspended by a long cord. Assume that the bullet remains in the block and that it swings 0.086m above the initial height. Calculate the velocity of the bullet when it strikes the wood.

Answer 1

261.3 m/s

Step-by-step explanation:

Mass of bullet=m=15 g=
`(15)/(1000)=0.015 kg`

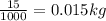
1 kg=1000g

Mass of block=M=3 kg

d=0.086 m

Total mass =M+m=3+0.015=3.015 kg

K.E at the time strike=Gravitational potential energy at the end of swing

`(1)/(2)(m+M)^2V^2=(m+M)gh`

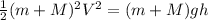
Using g=
`9.8m/s^2`

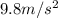
Substitute the values

`(1)/(2)(3.015)V^2=3.015* 9.8* 0.086`

`V^2=(2* 3.015* 9.8* 0.086)/(3.015)`

`V=√(2* 3.015* 9.8* 0.086)}`

`V=1.3m/s`

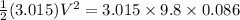
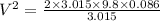
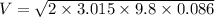
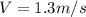
Velocity after collision=V=1.3 m/s

Velocity of block=v'=0

Using conservation law of momentum

`mv+Mv'=(m+M)V`

Using the formula

`0.015v+3(0)=3.015(1.3)`

`0.015v=3.015(1.3)`

`v^2=(3.015(1.3))/(0.015)=261.3`

`v=261.3 m/s`