Answer:
(a). The Final intensity is 126 times of initial intensity.
(b). The pressure amplitude increased is 11.22 times of initial pressure.
Step-by-step explanation:
Given that,
Sound level = 21 dB
(a). We need to calculate the increases increases
Using sound level equation
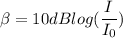
The intensity level for original sound level is
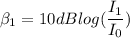
The intensity level for final sound level is
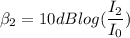
Subtract equation (I) from equation (2)...
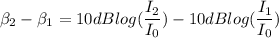

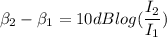
Put the value into the formula

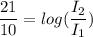
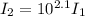
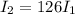
The Final intensity is 126 times of initial intensity.
(b). We need to calculate the pressure amplitude increased
Using formula of pressure

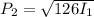

The pressure amplitude increased is 11.22 times of initial pressure.
Hence, (a). The Final intensity is 126 times of initial intensity.
(b). The final pressure amplitude is 11.22 times of initial pressure.