Question

A system consists of two components C1 and C2, each of which must be operative in order for the overall system to function. Let W1 and W2 be the events that components C1 and C2 work without failure for one day. The probabilities P(W1) and P(W2) are called the reliabilities of components C1 and C2. The probability P(W1W2) is called the reliability of the whole system. If P(W1) = 0.9 and P(W2) = 0.8, calculate the reliability of each system. Which of the systems has greater reliability. Attach a file with your solution approach.

Answer 1

The reliability of the first system to work is 0.72 whereas the reliability of the second system to work is 0.98.As the reliability of the second system is more than the first one so the second system is more reliable.

Explanation:

For first system as given in the attached diagram gives,

`P(W_1W_2)=P(W_1) * P(W_2)`

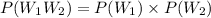
As the systems are independent.

The given data indicates that

• 
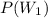  `P(W_1)` is given as 0.9
• 
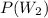  `P(W_2)` is given as 0.8

Now the probability of the system is given as

`P(W_1W_2)=P(W_1) * P(W_2)\\P(W_1W_2)=0.9 * 0.8\\P(W_1W_2)=0.72`

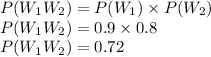
So the reliability of the first system to work is 0.72.

For the second system is given as

`P(W_1W_2)=1-P(W_1'W_2')`

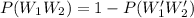
Where

• 
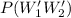  `P(W_1'W_2')` is the probability where both of the systems does not work. this is calculated as

`P(W_1'W_2')=P(W_1') * P(W_2')\\P(W_1'W_2')=(1-P(W_1)) * (1-P(W_2))\\P(W_1'W_2')=(1-0.9) * (1-0.8)\\P(W_1'W_2')=(0.1) * (0.2)\\P(W_1'W_2')=0.02`

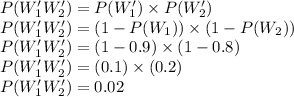
So now the probability of the second system is given as

`P(W_1W_2)=1-P(W_1'W_2')\\P(W_1W_2)=1-0.02\\P(W_1W_2)=0.98`

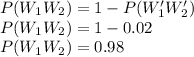
So the reliability of the second system to work is 0.98.

As the reliability of the second system is more than the first one so the second system is more reliable.