Question

A rigid tank initially contains 3kg of carbon dioxide (CO2) at a pressure of 3bar.The tank is connected by a valve to a frictionless piston-cylinder assembly located vertically above, initially containing 0.5 m^3 of CO2. The piston area is 0.1 m^2. Initially the pressure of the CO2 in the piston-cylinder assembly is 2 bar. The ambient pressure and temperature are 1 bar and 290 K. Although the valveis closed, a small leak allows CO2 to flow slowly into the cylinder from the tank. Owing to heat transfer, the temperature of the CO2 throughout the tank and the piston-cylinder assembly stays constant at 290K. You can assume ideal gas behavior for CO2.

Determine the following:

a. The total amount of energy transfer by work (kJ)
b. The total amount of energy transfer by heat (kJ)

Answer 1

Part a: The total amount of energy transfer by the work done is 54.81 kJ.

Part b: The total amount of energy transfer by the heat is 54.81 kJ

Step-by-step explanation:

Mass of Carbon Dioxide is given as m1=3 kg

Pressure is given as P1=3 bar =300 kPA

Volume is given as V1=0.5 m^3

Pressure in tank 2 is given as P2=2 bar=200 kPa

T=290 K

Now the Molecular weight of
`CO_2` is given as

M=44 kg/kmol

the gas constant is given as

`R=\frac{\bar{R}}{M}\\R=(8.314)/(44)\\R=0.189 kJ/kg.K`

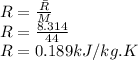
Volume of the tank is given as

`V=(mRT)/(P_1)\\V=(3 * 0.189 * 290)/(300 )\\V=0.5481 m^3`

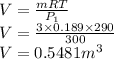
Final mass is given as

`m_2=(P_2V)/(RT)\\m_2=(200* 0.5481)/(0.189* 290)\\m_2=2 kg`

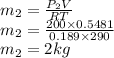
Mass of the CO2 moved to the cylinder

`m=m_1-m_3\\m=3-2=1 kg`

The initial mass in the cylinder is given as

`m_((cyl)_1)=(P_((cyl)_1)V_1)/(RT)\\m_((cyl)_1)=(200* 0.5)/(0.189 * 290)\\m_((cyl)_1)=1.82 kg`

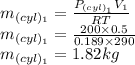
The mass after the process is

`m_((cyl)_2)=m_((cyl)_1)+m\\m_((cyl)_2)=1.82+1\\m_((cyl)_2)=2.82\\`

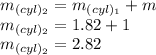
Now the volume 2 of the cylinder is given as

`V_((cyl)_2)=(m_((cyl)_2)RT)/(P_2)\\m_((cyl)_2)=(2.82* 0.189* 290)/(200)\\m_((cyl)_1)=0.774 m^3`

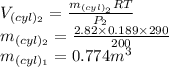
Part a:

So the Work done is given as

`W=P(V_2-V_1)\\W=200(0.774-0.5)\\W=54.81 kJ`

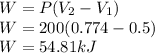
The total amount of energy transfer by the work done is 54.81 kJ.

Part b:

The total energy transfer by heat is given as

`Q=\Delta U+W\\Q=0+W\\Q=54.81 kJ`

As the temperature is constant thus change in internal energy is 0.

The total amount of energy transfer by the heat is 54.81 kJ