Question

A 4500-kg spaceship is in a circular orbit 160 km above the surface of Earth. It needs to be moved into a higher circular orbit of 360 km to link up with the space station at that altitude. In this problem you can take the mass of the Earth to be 5.97 × 1024 kg.

Answer 1

The work done is
`0.4*10^(10)\ J`.

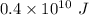Step-by-step explanation:

Given that,

Mass of space ship = 4500 kg

Distance = 160 km

Suppose How much work, in Joules, do the spaceship's engines have to perform to move to the higher orbit.

We need to calculate the total energy of the object at height 160 from the ground

Using formula of energy

`E = -(GmM_(e))/(2(r+h))`

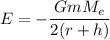
Put the value into the formula

`E=-(6.67*10^(-11)*5.97*10^(24)*4500)/(2(6378*10^(3)+160*10^(3)))`

`E=-13.70*10^(10)\ J`

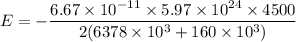
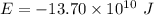
We need to calculate the total energy of the object at height 360 km from the ground

Using formula of energy

`E' = -(GmM_(e))/(2(r+h))`

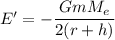
Put the value into the formula

`E'=-(6.67*10^(-11)*5.97*10^(24)*4500)/(2(6378*10^(3)+360*10^(3)))`

`E'=-13.29*10^(10)\ J`

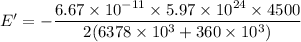
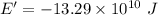
We need to calculate the work done

Using formula of work

`W=E'-E`

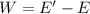
Put the value into the formula

`W=-13.29*10^(10)-(-13.70*10^(10))`

`W=0.4*10^(10)\ J`

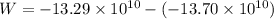
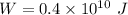
Hence, The work done is
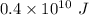`0.4*10^(10)\ J`.