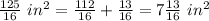Question

Please see picture below

Answer 1

The surface area is
`7(13)/(16)\ in^2`

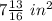
Explanation:

we know that

The surface area of a square pyramid is equal to the area of the square base plus the area of its four lateral triangular faces

The triangular faces are congruent

With the help of net, we can easily see the different sides, faces and angles of the square pyramid and calculate the surface area by finding the area of each face of the pyramid.

see the attached figure to better understand the problem

Remember that

`1(1)/(4)\ in=1+(1)/(4)=(5)/(4)\ in`

`2(1)/(2)\ in=2+(1)/(2)=(5)/(2)\ in`

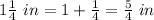
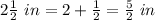
The surface area is equal to

`SA=((5)/(4))^2+4[(1)/(2)((5)/(4))((5)/(2))]`

`SA=(25)/(16)+(100)/(16)=(125)/(16)\ in^2`

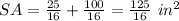
Convert to mixed number

`(125)/(16)\ in^2=(112)/(16)+(13)/(16)=7(13)/(16)\ in^2`