Question

A 27-year U.S. Treasury bond with a face value of $1,000 pays a coupon of 6.00% (3.000% of face value every six months). The reported yield to maturity is 5.6% (a six-month discount rate of 5.6/2 = 2.8%).a. What is the present value of the bond? Present value $ b. If the yield to maturity changes to 1%, what will be the present value? Present value $ c. If the yield to maturity changes to 8%, what will be the present value? Present value $ d. If the yield to maturity changes to 15%, what will be the present value? Present value $

Answer 1

(A) $1,055.35 (B) $2,180.53 (C) $780.07 (D) $412.08.

Step-by-step explanation:

The tenor of the bond is 27 years i.e. (27 * 2=) 54 periods of 6 months each (n).

Face Value (F) = $1,000

Coupon (C) = 6% annually = 3% semi annually = (3% * 1000 face value) = $30.

The Present Value (PV) of the Bond is computed as follows.

PV of recurring coupon payments + PV of face value at maturity

=
`(C(1-(1+r)^(-n)) )/(r) + (F)/((1+r)^(n))`

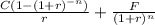
A) Yield = 5.6% annually = 2.8% semi annually.

`PV = (30(1-(1.028)^(-54)) )/(0.028) + (1,000)/((1.028)^(54))`

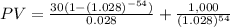
= 830.25 + 225.10

= $1,055.35.

B) Yield = 1% annually = 0.5% semi annually.

`PV = (30(1-(1.005)^(-54)) )/(0.005) + (1,000)/((1.005)^(54))`

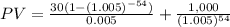
= 1,416.64 + 763.89

= $2,180.53.

C) Yield = 8% annually = 4% semi annually.

`PV = (30(1-(1.04)^(-54)) )/(0.04) + (1,000)/((1.04)^(54))`

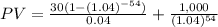
= 659.79 + 120.28

= $780.07.

D) Yield = 15% annually = 7.5% semi annually.

`PV = (30(1-(1.075)^(-54)) )/(0.075) + (1,000)/((1.075)^(54))`

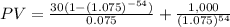
= 391.95 + 20.13

= $412.08.