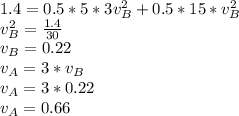Question

A 30 cm spring with constant 70 N/m is compressed to 10 cm and placed between two carts. Cart A mass m5kg andmp is unknown. Initially the system is at rest. After it is released it is observed that cart A has three times the velocity of cart B. 1. a) What force must be exerted initially to keep the spring compressed? b) What is the work done to compress the spring? c) By considering conservation of momentum determine the mass m d) By considering conservation of energy find the velocities of the carts A and B after the spring is released

Answer 1

Part A
`F = 14` Newton

Part B
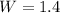`W = 1.4` Joules

Part C
`m_B = 15 Kg`

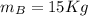
Part D

`v_ A = 0.22\\v_B= 0.66`

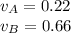
Step-by-step explanation:

Part A

Force in a spring is equal to the product of spring constant and displacement

Thus,

`F = kx\\F = 70 * 0.2\\`

`F = 14` Newton

Part B

Work done to compress the spring

`(1)/(2) kx^2\\= 0.5 * 0.7 * 0.2 * 0.2\\= 1.4 J`

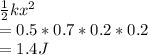
Part C

Given that velocity of cart A becomes three time the velocity of cart B

As per the conservation of momentum equation

`m_Av_A = m_Bv_B\\m_A * 3v_B= m_B* v_B\\m_B = m_A * 3\\m_B = 5 * 3\\m_B = 15`

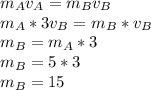
Part D

Substituting the given values we get

`1.4 = 0.5 * 5 * 3v_B^2 + 0.5 * 15 * v_B^2\\v_B^2 = (1.4)/(30) \\v_B = 0.22\\v_A = 3 * v_B\\v_A = 3* 0.22\\v_A = 0.66`