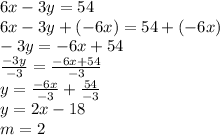Answer:
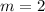
Explanation:
- Before beginning, I'm going to show the guideline for slope-intercept form for linear equations:
· Slope-Intercept Form:
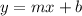
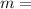 slope; the rotation of the line
slope; the rotation of the line
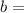 the line's
the line's
 -intercept; where the line hits the
-intercept; where the line hits the
 -axis.
-axis.
· Both
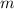 and
and
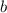 are constant integers whose value ranges from -∞ ⇒ ∞, all real numbers.
are constant integers whose value ranges from -∞ ⇒ ∞, all real numbers.
·
 and
and
 are values that depend on each other's value;
are values that depend on each other's value;
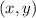 is how you would see them written on a number line.
is how you would see them written on a number line.
- With this in mind, let's look at our current equation.
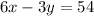
- It seems that our equation is not in a form that could easily show us what it's rotation is, slope, or where it hits the
 -axis, so we're going to have to rearrange our equation so that it follows the slope-intercept guideline shown above.
-axis, so we're going to have to rearrange our equation so that it follows the slope-intercept guideline shown above.
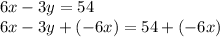
- My first step was to move any values that are neither being multiplied nor divided by
 to the other side of the equation. In this case,
to the other side of the equation. In this case,
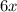 is being added to
is being added to
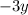 , so by adding the reciprocal of
, so by adding the reciprocal of
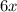 to both sides, I can move it to the other side.
to both sides, I can move it to the other side.
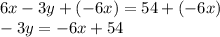
- Now our equation is starting to look somewhat like the guideline for slope-intercept form; all we need to do now is get rid of the
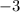 next to the
next to the
 by dividing.
by dividing.
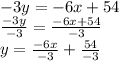
- Almost there. All that's left is simplification and we're done!
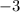 goes into
goes into
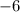 two times, and
two times, and
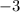 goes into
goes into
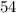 negative eighteen times, so our final, simplified equation is:
negative eighteen times, so our final, simplified equation is:
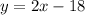
- By looking at our guideline,
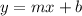 where
where
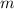 is slope and
is slope and
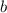 is the
is the
 -intercept, we can determine that:
-intercept, we can determine that:
The slope of
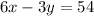 is
is
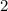 .
.
Uninterrupted Work: