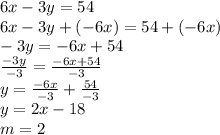Answer:
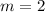
Explanation:
- Before beginning, I'm going to show the guideline for slope-intercept form for linear equations:
· Slope-Intercept Form:
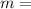slope; the rotation of the line
the line's
-intercept; where the line hits the
-axis.
· Both
and
are constant integers whose value ranges from -∞ ⇒ ∞, all real numbers.
·
and
are values that depend on each other's value;
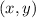is how you would see them written on a number line.
- With this in mind, let's look at our current equation.
- It seems that our equation is not in a form that could easily show us what it's rotation is, slope, or where it hits the
-axis, so we're going to have to rearrange our equation so that it follows the slope-intercept guideline shown above.
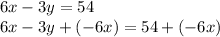
- My first step was to move any values that are neither being multiplied nor divided by
to the other side of the equation. In this case,
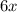is being added to
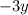, so by adding the reciprocal of
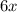to both sides, I can move it to the other side.
- Now our equation is starting to look somewhat like the guideline for slope-intercept form; all we need to do now is get rid of the
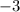next to the
by dividing.
- Almost there. All that's left is simplification and we're done!
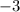goes into
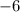two times, and
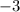goes into
negative eighteen times, so our final, simplified equation is:
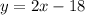
- By looking at our guideline,
where
is slope and
is the
-intercept, we can determine that:
The slope of
is
.
Uninterrupted Work:
