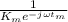Question

A common problem in over-the-air television signal transmission is multipath distortion of the received signal due to the transmitted signal bouncing off structures. Typically a strong main signal arrives at some time and a weaker ghost signal arrives later. So if the transmitted signal is x,() the recieved signal is where >> Kg and 1.x, . 1 What is the transfer function of this communication channel? 2. What would be the transfer function of an equalization system that would compensate for the effects of multipath?

Answer 1

Part 1: The transfer function of the system is given as
`K_me^(-j\omega t_m)+K_ge^(-j\omega t_g)`

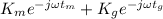
Part 2: The transfer function of the equalization system is
`(1)/(K_me^(-j\omega t_m))`

Step-by-step explanation:

Part 1

`TF_(sys)=(FT[OP])/(FT[IP])\\TF_(sys)=(FT[K_mx_t(t-t_m)+K_gx_t(t-t_g])/(FT[x(t)])\\TF_(sys)=(K_mx_t(\omega)e^(-j\omega t_m)+K_gx_t(\omega)e^(-j\omega t_g))/(x_t(\omega))\\TF_(sys)=(x_t(\omega)[K_me^(-j\omega t_m)+K_ge^(-j\omega t_g)])/(x_t(\omega))\\TF_(sys)=K_me^(-j\omega t_m)+K_ge^(-j\omega t_g)`

The transfer function of the system is
`K_me^(-j\omega t_m)+K_ge^(-j\omega t_g)`

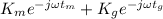
Part 2

As the equalization system is a system which compensate the effects of the system thus if the transfer function of the equalization system is given as
`TF_(eq)`

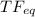
Than

`TF_(sys) * TF_(eq)=1`

or

`TF_(eq)=(1)/(TF_(sys) )\\TF_(eq)=(1)/(K_me^(-j\omega t_m)+K_ge^(-j\omega t_g))`

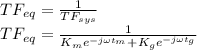
As it is given that Km>>Kg thus ignoring the values with Kg multiplier yields

`TF_(eq)=(1)/(K_me^(-j\omega t_m))`

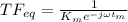
So the transfer function of the equalization system is
`(1)/(K_me^(-j\omega t_m))`