Question

In a multiple regression analysis involving 4 predictor variables, and 25 observations, the total sum of squares is 800, and the error sum of squares is 200. The value of the F-test statistic for testing the usefulness of this model must be _______.

(A) 12
(B) 15
(C) 32
(D) 50
(E) 200

Answer 1

`MS_(regression)= (SS_(reg))/(k)= (600)/(4)=150`

`MS_(error)= (SSE)/(N-k-1)= (200)/(20)= 10`

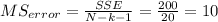
And then the F statistic would be given by:

`F= (MSR)/(MSE)= (150)/(10)= 15`

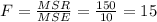
And the correct answer would be:

(B) 15

Explanation:

Previous concepts

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

When we conduct a multiple regression we want to know about the relationship between several independent or predictor variables and a dependent or criterion variable.

Solution to the problem

If we assume that we have
`k` independent variables and we have
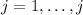`j=1,\dots,j` individuals, we can define the following formulas of variation:

`SS_(total)=\sum_(j=1)^n (y_j-\bar y)^2 = 800`

`SS_(regression)=SS_(model)=\sum_(j=1)^n (\hat y_(j)-\bar y)^2`

`SS_(error)=\sum_(j=1)^n (y_(j)-\hat y_j)^2 =200`

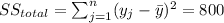
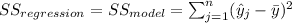
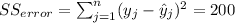
And we have this property

`SST=SS_(regression)+SS_(error)`

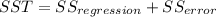
So then we have that:

`SST_(regression)= 800-200= 600`

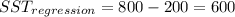
The degrees of freedom for the model on this case is given by
`df_(model)=df_(regression)=k=4` where k =4 represent the number of variables.

The degrees of freedom for the error on this case is given by
`df_(error)=N-k-1=25-4-1= 20`. Since we know k we can find N.

And the total degrees of freedom would be
`df=N-1=25 -1 =24`

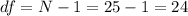
We can calculate the mean squares for the regression and the error like this:

`MS_(regression)= (SS_(reg))/(k)= (600)/(4)=150`

`MS_(error)= (SSE)/(N-k-1)= (200)/(20)= 10`

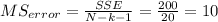
And then the F statistic would be given by:

`F= (MSR)/(MSE)= (150)/(10)= 15`

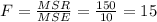
And the correct answer would be:

(B) 15