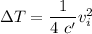Question

A lead bullet of mass m traveling at vi penetrates a wooden block and stops.

Assuming that 50% of the initial kinetic energy of the bullet is converted into thermal energy in the bullet and the specific heat of lead is c, write an expression that would allow you to determine the bullet's temperature increase.

Express your answer in terms of the variables m, vi and c.

Answer 1

`\Delta T=(1)/(4\ c )v_i^2`

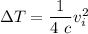
Step-by-step explanation:

Given that

mass of the bullet = m

Speed of the bullet = vi

Therefore the kinetic energy of the bullet KE will be

`KE=(1)/(2)mv_i^2`

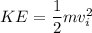
Given that 50 % of the kinetic energy is converted into thermal energy.

KE'= 0.5 KE

The thermal energy Q is given as

Q= m c ΔT

Q=Heat

m=mass

c=specific heat capacity

ΔT=Temperature difference

Therefore we can say that

Q= KE'

`Q=0.5* (1)/(2)mv_i^2`

`m\ c\ \Delta T=0.5* (1)/(2)mv_i^2`

`c\ \Delta T=0.5* (1)/(2)v_i^2`

`\Delta T=(1)/(4\ c)v_i^2`

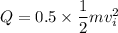
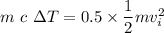
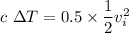
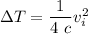
Therefore the increase in temperature is given as

`\Delta T=(1)/(4\ c' )v_i^2`