Answer:
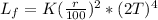
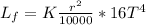
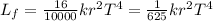

So then we see that the final luminosity decrease by a factor of 625 so then the correct answer for this case would be:
B. Decreases by a factor of 625
Step-by-step explanation:
For this case we can use the formula of luminosity in terms of the radius and the temperature given by:
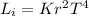
Where L_i = initial luminosity, r= radius and T = temperature.
We know that we decrease the radius by a factor of 100 and the temperature increases by a factor of 2 so then the new luminosity would be:
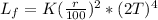
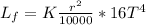
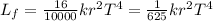

So then we see that the final luminosity decrease by a factor of 625 so then the correct answer for this case would be:
B. Decreases by a factor of 625