Answer:
The standard deviation of the sample mean decreases from 1.43 to 0.5 as n increases from 6 to 49.
Explanation:
The standard deviation of the sample mean is given by the following formula:
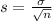
In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
In this problem, we have that:
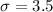
How is the standard deviation of the sample mean changed when the sample size is increased from n=6 to n=49?
n = 6
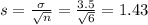
n = 49
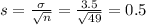
The standard deviation of the sample mean decreases from 1.43 to 0.5 as n increases from 6 to 49.