Answer:
The x-component and y-component of the velocity of the cruise ship relative to the patrol boat is -5.29 m/s and 0.18 m/s.
Step-by-step explanation:
Given that,
Velocity of ship = 2.00 m/s due south
Velocity of boat = 5.60 m/s due north
Angle = 19.0°
We need to calculate the component
The velocity of the ship in term x and y coordinate
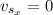
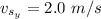
The velocity of the boat in term x and y coordinate
For x component,

Put the value into the formula
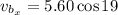
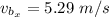
For y component,

Put the value into the formula
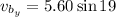
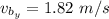
We need to calculate the x-component and y-component of the velocity of the cruise ship relative to the patrol boat
For x component,
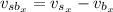
Put the value into the formula
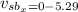
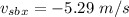
For y component,
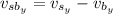
Put the value into the formula
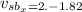
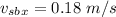
Hence, The x-component and y-component of the velocity of the cruise ship relative to the patrol boat is -5.29 m/s and 0.18 m/s.