Question

A survey conducted by the Consumer Reports National Research Center reported, among other things, that women spend an average of 1.2 hours per week shopping online. Assume that hours per week shopping online are Poisson distributed. If this survey result is true for all women and if a woman is randomly selected,

a. What is the probability that she would shop exactly two hours online over a one-week period?
b. What is the probability that a woman would shop four or more hours online during a one-week period?
c. What is the probability that a woman would shop fewer than five hours in a three-week period?

Answer 1

(a) The probability that a randomly selected woman shop exactly two hours online is 0.217.

(b) The probability that a randomly selected woman shop 4 or more hours online is 0.0338.

(c) The probability that a randomly selected woman shop less than 5 hours online is 0.9922.

Explanation:

Let X = time spent per week shopping online.

It is provided that the random variable X follows a Poisson distribution.

The probability function of a Poisson distribution is:

`P (X=x)=(e^(-\lambda)\lambda^(x))/(x!) ;\ x=0,1,2,...`

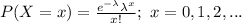
The average time spent per week shopping online is, λ = 1.2.

(a)

Compute the probability that a randomly selected woman shop exactly two hours online over a one-week period as follows:

`P (X=2)=(e^(1.2)(1.2)^(2))/(2!) =0.21686\approx0.217`

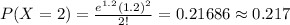
Thus, the probability that a randomly selected woman shop exactly two hours online is 0.217.

(b)

Compute the probability that a randomly selected woman shop 4 or more hours online over a one-week period as follows:

P (X ≥ 4) = 1 - P (X < 4)

= 1 - P (X = 0) - P (X = 1) - P (X = 2) - P (X = 3)

`=1-(e^(1.2)(1.2)^(0))/(0!)-(e^(1.2)(1.2)^(1))/(1!)-(e^(1.2)(1.2)^(2))/(2!)-(e^(1.2)(1.2)^(2))/(3!)\\=1-0.3012-0.3614-0.2169-0.0867\\=0.0338`

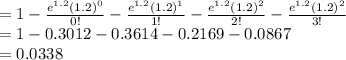
Thus, the probability that a randomly selected woman shop 4 or more hours online is 0.0338.

(c)

Compute the probability that a randomly selected woman shop less than 5 hours online over a one-week period as follows:

P (X < 5) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4)

`=(e^(1.2)(1.2)^(0))/(0!)+(e^(1.2)(1.2)^(1))/(1!)+(e^(1.2)(1.2)^(2))/(2!)+(e^(1.2)(1.2)^(3))/(3!)+(e^(1.2)(1.2)^(4))/(4!)\\=0.3012+0.3614+0.2169+0.0867+0.0260\\=0.9922`

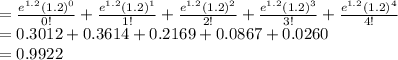
Thus, the probability that a randomly selected woman shop less than 5 hours online is 0.9922.